Converting R code to Python: A Test

Background

I’ve been using R as my statistics programming environment for decades. In fact, I started out using its predecessor, an earlier (non-open source) program called S. In the last 10 or so years, the role of data scientist has appeared, and in the main, data scientists use the Python programming language, which comes with its own many statistical libraries. In terms of statistics, there’s a huge overlap in the capabilities of R and Python — pretty much anything you can do in R, you can do in Python, and vice-versa. Of course, Python is also used everywhere these days in places you wouldn’t consider using R, e.g. building apps or websites.

In 2020, I completed a few Python modules at DataCamp, but haven’t needed to use it much since. However, Python is pretty much the #1 requirement when it comes to applying for data science positions, so I need to get comfortable with it.

Where I have my own (fairly extensive) library of R functions for various modelling, credit risk and maths purposes, it’d be nice to port all that code to Python — and even nicer if it could be done with as little effort as possible on my part! 😀 So let’s see how we get on with a small-ish function.

The function in R

In the 90s, my MSc dissertation was concerned with exact tests in contingency tables: see the wiki entry Fisher’s exact test for more details. In the PhD thesis of Dr Danius Michaelides, Exact Tests via Complete Enumeration: A Distributed Computing Approach, he describes an algorithm that enumerates integer partitions, subject to constraints (see Section 2.3.2 and Figure 2.2). This algorithm is used in the enumeration of contingency tables with fixed margins.

I’ve recreated this algorithm from his description. The function partitions_with_constraints takes two parameters: v, an array of maximum values, and N, the integer to be partitioned; and returns a matrix of all the possible partitions.

partitions_with_constraints <- function(v, N)
{
  vl = length(v);
  stopifnot( vl >= 2 );
  stopifnot( all(v > 0) );
  stopifnot( N <= sum(v) );

  cells = rep(NA,vl);

  res = c();

  i = 1;

  while (i > 0)
  {
    allocated = if(i==1) 0 else sum(cells[1:(i-1)]);
    remaining = N - allocated;
    
    if (i == vl) {

      # We're at the last cell,
      # which can only be the amount remaining.
      # Add the cells array to our results.

      cells[i] = remaining;
      res = rbind(res, cells);
      i = i - 1

    } else {

      if (is.na(cells[i])) {
        # Set the cell to the minimum possible
        cells[i] = max(0, remaining - sum(v[(i+1):vl]));
      } else {
        # Otherwise, increment
        cells[i] = cells[i] + 1
      }
      cell.max = min(remaining, v[i]);

      if (cells[i] > cell.max) {
        # We've hit the maximum; blank the cell, and move back one
        cells[i] = NA;
        i = i - 1;
      } else {
        i = i + 1;
      }
    }
  }

  # Restore the indices on the rows:
  res = matrix(res, nrow=dim(res)[1], byrow=F);
  return(res);
}

If we run it using the example from the thesis, we get:

partitions_with_constraints(c(3,1,3),4);
     [,1] [,2] [,3]
[1,]    0    1    3
[2,]    1    0    3
[3,]    1    1    2
[4,]    2    0    2
[5,]    2    1    1
[6,]    3    0    1
[7,]    3    1    0

To explain the output in words: there are 7 ways in which we can partition the number 4 into sums of three numbers, where the first number is between 0 and 3, the second number is between 0 and 1, and the third number is between 0 and 3.

Converting the code with Copilot

For the conversion, I used Microsoft Copilot. (There is a ‘pro’ version, but I’m using the free website version.) If you google Copilot, it seems to be referred to mainly as a ‘chatbot’, but that term feels rather inadequate — so I asked Copilot how to describe itself! It said “Microsoft Copilot is an AI companion designed to assist users by providing information, answering questions, and engaging in conversation.” An ‘AI companion’ is a better description, I think.

Into the ‘Ask me anything’ box, I wrote “Please convert this R function into Python:” and pasted in the code from above. Within a few seconds, it returned the Python code you see below.

The function in Python

Here’s the code that Copilot returned:

import numpy as np

def partitions_with_constraints(v, N):
    vl = len(v)
    assert vl >= 2
    assert all(i > 0 for i in v)
    assert N <= sum(v)

    cells = [None]*vl
    res = []

    i = 1

    while i > 0:
        allocated = 0 if i == 1 else sum(cells[0:i-1])
        remaining = N - allocated

        if i == vl:
            cells[i-1] = remaining
            res.append(cells[:])
            i -= 1
        else:
            if cells[i-1] is None:
                cells[i-1] = max(0, remaining - sum(v[i:vl]))
            else:
                cells[i-1] += 1
            cell_max = min(remaining, v[i-1])

            if cells[i-1] > cell_max:
                cells[i-1] = None
                i -= 1
            else:
                i += 1

    return np.array(res)

It also output some additional text, describing how the primitive function calls are translated: This Python function should behave similarly to your R function. Please note that Python uses 0-based indexing, unlike R which uses 1-based indexing. This means that some adjustments were needed in the translation. Also, Python does not have a direct equivalent to R’s NA, so None is used instead. The rbind function in R is replaced with list append and conversion to a numpy array in Python. The stopifnot function in R is replaced with assert in Python. The all and sum functions in Python behave similarly to their counterparts in R. The length function in R is replaced with len in Python. The rep function in R is replaced with list multiplication in Python. The max and min functions in Python behave similarly to their counterparts in R.

For me, the most impressive thing is the conversion of arrays from 1-based (i.e. arrays are indexed starting from 1 in R) to 0-based (as in Python, like e.g. C/C++); that wasn’t specified anywhere in the instructions, it just ‘knew’ to do it.

I often use one of the following online sites to run Python (if the code isn’t too big):

• Online Python
• Python Online Compiler

I used the first one, pasting the code in, plus the call to the function with the same parameters as in the R version:

print(partitions_with_constraints([3,1,3],4))

[[0 1 3]
 [1 0 3]
 [1 1 2]
 [2 0 2]
 [2 1 1]
 [3 0 1]
 [3 1 0]]

which you can check is the same data as the R version, only the output formatting is different.

Full disclosure: the code didn’t run first time — I’d made a tiny mistake in one of my assertions, that Copilot just translated without picking up on it. And when it did run, there was no output, because I’d forgotten the print(…) around the function call. But these were very minor issues, fixed in seconds.

---

Copilot generating Python from a description

I want to present another instance of Copilot helping with coding; in this case, not a conversion, but coding an algorithm from a description of what the algorithm should do.

As I’ve mentioned before (in the post Practical queries using binary operations), I occasionally toy around with a Sudoku solver I’ve written in SQL. There’s one piece of cell-checking code I haven’t written yet, so could Copilot write it for me?

My prompt:“I am writing a Sudoku solver. For each remaining cell, I have a list of possible values for that cell. For example, I have a row where four cells have been filled in: 1,4,6 and 8. The remaining possible cell values are (3,7),(2,3,5),(2,3,9),(5,9),(5,7,9) , where parentheses delimit cells. What algorithm can I use to find all possible combinations of cell values? E.g. for my example here, 3,2,9,5,7 is a possibility.”

Copilot wrote: You can use a recursive backtracking algorithm to find all possible combinations of cell values. Here’s a Python function that does this:

def solve_sudoku(possible_values, index=0, solution=[]):
    if index == len(possible_values):
        print(solution)
        return

    for value in possible_values[index]:
        if value not in solution:
            solve_sudoku(possible_values, index + 1, solution + [value])

possible_values = [(3,7),(2,3,5),(2,3,9),(5,9),(5,7,9)]
solve_sudoku(possible_values)

Looks promising… here’s the output when I run the code at Online Python:

[3, 2, 9, 5, 7]
[3, 5, 2, 9, 7]
[7, 2, 3, 5, 9]
[7, 2, 3, 9, 5]
[7, 3, 2, 5, 9]
[7, 3, 2, 9, 5]

It worked, first time.

Then, I asked if it could convert the code to SQL:

SQL is not designed for this type of recursive computation... That being said, you can use recursive Common Table Expressions (CTEs) in SQL for some types of recursive problems. However, the problem you’re trying to solve involves backtracking, which is not straightforward to implement in SQL.

Oh well, you can’t win them all! [I’m not entirely sure how I’m going to convert it to SQL, but the Python code has given me some ideas, so that’s better than nothing.]

---

Final thoughts

This all worked much better than I thought it would, and the odds are very good that I can convert all my R code to Python without too much work. Sure, the algorithms above aren’t that complicated, but none of my R code is that complicated; most of the functions are wrappers around calls to R libraries. If direct conversion doesn’t work, I can try asking Copilot to recreate the code from a text description of the input/output.

Fun converting to integers in R

If you work on the programming side of finance, then I expect that you share my sentiment that rounding errors are the bane of our lives. I was writing a function in R to process the calculations in a loan schedule (more on that soon, watch this space), and was rather quickly overwhelmed with figures not adding up. So, I thought it would be a good idea to do as many of the calculations in pence (rather than pounds) as possible; then that way I was only dealing with integers, not floating point numbers.

Why didn’t I use a decimal datatype? Because there isn’t one in R! (See the end of this post.)

Converting to integer values for pence should have solved all the problems, but I was still getting calculation errors. What was going wrong?

Here’s a value which is the un-rounded total interest amount due on a loan:

interest  = 621.5518100862391293;

This amount is in pounds — the way that interest (and/or payments) are usually calculated, it’s inevitable that the amount won’t be a whole number of pence. Clearly, we can’t charge 0.181 etc. of a penny, so we round it down. (Good practice says you should always round interest values in the customer’s favour.)

I want to turn that figure from pounds into pence; here I’m after a value of 62155 pence.

I can use the floor function to remove the fractional part of the pence (everything less than 1p):

interest_2dp = floor(interest * 100) / 100;
interest_2dp
[1] 621.55

Convert it to pence:

interest_pence = 100 * interest_2dp;
interest_pence
[1] 62155

All good so far.

Now, the datatype of the variable interest_pence is:

class(interest_pence)
[1] "numeric"

but my code is expecting an integer. There’s a function, as.integer, in R to do the conversion (that discards anything after the decimal point):

interest_pence_int = as.integer(interest_pence);

which has the value:

interest_pence_int
[1] 62154

Wait, what? 62154 not 62155? Where’s the penny gone?

Well, it’s because our previous values haven’t been displayed to full accuracy. We can easily show this:

interest_pence - 62155
[1] -7.275958e-12

Therefore interest_pence is slightly less than 62155 — in other words 62154 plus some number that’s nearly-but-not-quite one. Hence when we convert to integer, it discards the fractional part, and we get 62154.

The fix

Basically, it seems this is caused by the division by 100, then the multiplication by 100. If we remove this redundancy, then we get:

floor(interest*100)
[1] 62155
as.integer(floor(interest*100))
[1] 62155

I’m not claiming that all the rounding errors in my code are fixed forever by doing this, I know better than that! However, things are looking much better.

Some notes:

• This all looks a bit trivial, why didn’t I spot it straight away? Simply because in my code, other things were happening between the declarations of interest_pence and interest_pence_int, they were several lines apart.
• This is all very similar to a previous post, where essentially the same thing was happening in SQL: Floats may not look distinct
• I did spend a long time messing with converting the numbers to strings (via sprintf) then truncating them, to see if I could get round the problem that way; but it just made things worse, because sprintf does rounding of its own.

---

Decimals in R

Sounds unlikely, but it’s true: R doesn’t have a native decimal datatype.

I found this answer to the stackoverflow post “Is there a datatype “Decimal” in R?”, which has some code to create a decimal structure (using an underlying integer64 type), but it didn’t work for me: the line d + as.decimal(0.9) returned an integer64 type, rather than the expected decimal.

There’s also this repo on GitHub, but I didn’t try it out – I didn’t want to introduce more libraries if I could help it.

Another avenue I could’ve tried is using the GNU Multiple Precision Arithmetic package, but again, probably overkill for something that should be so simple!

Things That Could Have Been (Part Three): The Daily Journal

This is part three of four mini-projects that nearly made it. Part One, “Process flow and DiagrammeR” is here. Part Two, “Better credit file summaries” is here.

---

The Daily Journal

In more than one finance company I’ve worked at, the Credit Risk and MI/BI departments are expected to be all-seeing and all-knowing, and they will have input into every aspect of the business^*. Which means they need lots of data, and lots of reports, charts and figures.

^* It’s not unusual for the Head of Credit Risk to be more of a hands-on, operational role, overseeing every part of the process in detail — authorising website changes, training collections teams, liaising with external auditors, etc.

The credit risk department is expected to create a monthly pack showing (and commenting on) all sorts of stats, from basic “number of applications”, “proportion of apps paid out”, “total money in / out”, down to the fine detail of how each variable in a scorecard is performing. Several years ago, while I was creating this monthly pack for the company I worked for, I realised that (a) it could be largely automated — after all, my scorecard build documents are automated (using the same tools); and (b) if it’s automated, you could have a version that included much more information.

Thus was born The Daily Journal: a very large document that contained hundreds and hundreds of graphs showing the performance of pretty much every credit risk metric — from basic stuff like application rates and maturity rates, to more niche measures like population stability index values for individual scorecard variables; shown over various time periods (e.g. ‘Last 30 days’, ‘Last 3 years’), divided into as many sub-populations as made sense (e.g. new customers vs old, homeowners vs renters, married vs single, by age range, etc.)

Basically, the Journal was to be a data bible — anything someone could reasonably want to know about the business’s operational performance, it’d be in there somewhere! So I started putting it together…

Examples

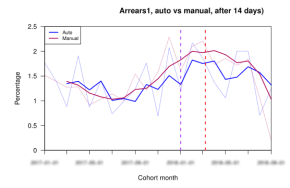
The last version of the document in development ran to over a hundred pages. Below are a few example graphs from that document:

Note that there were only 6 or so basic types of graph needed.

Benefits

At first thought, a huge document like this might seem like overkill. But there were several obvious benefits:

1. Historics. Sometimes, it’s not easy to generate data ‘as it looked in the past’. For one, most dev teams don’t factor this into their database builds. Also, code changes all the time, and it can be nigh on impossible to work out how a system operated X years ago. But with the Journal, we could look at old ‘editions’ and see exactly how things were. (And of course, fixed documents can’t change, which you can’t say about live reports)
2. It’s somewhere to keep important milestones/dates, and they could be automatically added to graphs. E.g. the release of new scorecard, acquiring a new marketing partner, launch of a new application system, etc. (That’s what the vertical dotted lines are in the examples.)
3. Similarly, manual commentary can be included. Either by using ‘include’ files, or straight from a database.
4. It could be an incredibly useful introduction for people new to the business, getting them talking about how things work, and even suggesting additions to the document.
5. I wanted the document to be available to the wider business, so anyone who needed to could access it and answer their own questions. Not everyone’s happy with tools like Power BI, but anyone can open a PDF.

How it was built: Sweave

I built the document using Sweave (R Studio: Using Sweave and knitr), which allows you to build documents by embedding R code within (a venerable typesetting language, much used in academia — see here). Because so much of the code was automated (and we were using our nice ‘clean’ database, see previous posts), and the graphs were all very similar, it didn’t take much effort to generate – it was just a matter of coding “all the levels of variable A over time, split out by variable B (and maybe C)”.

Here’s some pseudo-code to help get the point across:

dataFrame = CreateDataFrame("SELECT CustomerType, AgeBand, [Day], COUNT(1) AS Total
	FROM app.Application WHERE PaidOut >= '2019Jan01'
	GROUP BY CustomerType, AgeBand, [Day]")

For(customerType in levels(dataFrame.CustomerType))
For(ageBand in levels(dataFrame.AgeBand))
	Print "\section{Customer: " + customerType + ", Age: " + ageBand + ")"
	DrawGraph subset(dataFrame, (CustomerType = customerType) & (AgeBand = ageBand))
Next
Next

The above code could generate dozens of graphs.

Arguments against

Not that I got to the point where people could criticise the need for it, but pre-empting some arguments anyway…

Couldn’t you achieve the same results using Power BI?
Sort of. I saw the Journal as a companion to the live reports — it represented the past, whereas most reports are largely about the present and/or recent past. (Also, as mentioned above, sometimes it’s just easier to open a PDF.)

Wasn’t navigating around the document a pain?
builds tables of contents automatically, plus setting up links to jump around PDFs is easy. And LaTeX is so flexible, you could colour-code pages/tabs. If the document truly got too unwieldy, it’d be simple to set up a separate build process that had a curated selection of the pages, maybe a document for each department.

Surely not every graph or cross-tab is interesting?
Of course, and it’s trivial to exclude uninteresting variations.

Wasn’t the file huge?
Not really: under 5 MB. It was all text and embedded PNGs. (I used to work at a company that treated 250 MB Excel spreadsheets as ‘the norm’, so…)

Didn’t this take ages to make?
No, I think it took a few days, most of which was faffing around with colours, line widths and getting legends in the correct place on the graphs! The underlying data already existed, correctly indexed, this was just churning out graphs (and simple tables) in loops. The document was really just an expanded version of the monthly credit risk report — nearly all the ‘grunt work’ had been done already. Plus, it also covered quite a few recurring ad-hoc requests for stats.

---

How far did I get? About 95% of the way to the initial release. More urgent work got in the way, and it fell by the wayside. The usual!

Future plans: Lots more credit risk-related graphs and tables. As mentioned above, including manual commentary on graphs, and possibly department specific versions if required.

Things That Could Have Been (Part One): Process flow and DiagrammeR

You’ll be unsurprised to read that not everything I’ve worked on has made it into a live production environment. It happens — projects are abandoned for reasons of resource, time or requirement, and every seasoned developer is used to it. In this post, and the next three, I’m going to present four mini-projects that were the closest to making it ‘into live’. One day, I hope I’ll get the chance to resurrect them in some form.

---

Process flow and DiagrammeR

Nearly every company I’ve worked at in the past 20 years had, or was in the process of building, (*drum roll, deep resonant voice*) The Funnel. It’s a completely obvious concept: at the top of the funnel, start with all your potential customers (people you market to/contact, or applications, say). Then for each step of the process, show how many customers are left at each stage.

For a loans company, we’d have something like:

Clearly, this is only a very high-level overview, and by design leaves out fine details.

Here’s a slightly more interesting example on the same theme:

This shows us the process flow (aka workflow) for the initial part of the system, from application, via credit check, to the Affordability stage. This sort of flow diagram isn’t a replacement for the funnel, it’s an expanded, more detailed, view.

I made the above example using a wonderful R package called DiagrammeR, which is very straightforward to code for. More visual examples can be found here.

Real-life workflows

Below are two screenshots of actual workflows, for new and existing customers, taken from a real-life lender. The first stage is application, the last is payout. As you can see, the flows are quite complex; when I showed them these pictures, management were rather surprised at how complex the workflow had gotten.

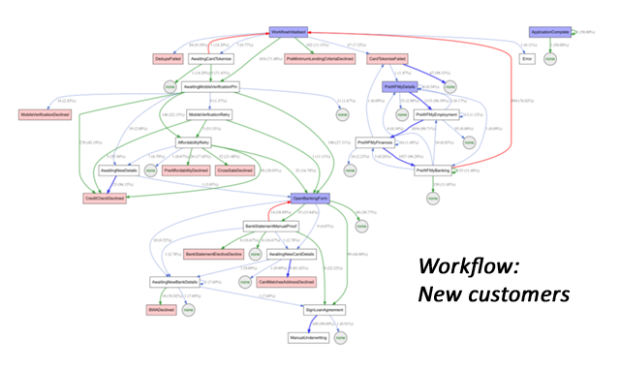
Both diagrams were generated automatically using the DiagrammeR package. The total amount of code required was surprisingly small: a couple of dozen lines of SQL, pulling from our ‘clean’ database^*, and a few dozen lines of R. The intent was to generate these diagrams (and various department-specific versions) on a schedule, and distribute them around the business, in order to:

1. Get a better understanding of how applications moved through the business
2. Help explain to non-technical staff what was going on ‘behind the scenes’
3. Look for opportunities for improvement to the application process
4. Keep an eye out for potential issues

In short, it made the invisible visible, which could only be a good thing.

* We had a database that was a cleaned-up and nicely re-organised version of the live data. It wasn’t a warehouse, as such, but it made common data requests much simpler.

 

Creating extra value from string data

In the previous post, I referred to a sales dataset that I’m currently working on. It has plenty of records (hundreds of thousands of rows), but not many variables (columns / fields). In order to build a good predictive model over a dataset that has a limited number of variables, sometimes you have to get creative; here, I’m going to describe just one of the ways I’ve “added value” (as they say) to the data.

In our dataset, we have addresses: Lines 1-5 and Postcode. Usually, what we do with address data is match it to other richer datasets by postcode — for example, you can buy sociodemographic data that will tell you about the composition of the population in that postcode: what the average earnings are, what proportion of people read a newspaper, all manner of interesting data points. In our case, there are no other datasets, so we have to make do with what we have.

With a bit of work (and cribbing from wikipedia), we can easily map the postcodes to regions and countries, which are always useful variables. And, as per the previous post, we can calculate distances to (say) major towns or distribution hubs. But what else?

Well, we can actually extract a fair bit of value from the address string data itself. I know from previous experience that the number of the house/building in the address can be predictive; from a consumer lending dataset a few years ago, it turned out that lower house numbers had better payback rates. (Maybe streets in well-off areas have fewer houses, which means that a house number of ‘765’ has to be in a less well-off area.) But what about the words themselves? As you’d expect, there are many common words in the first lines of addresses: Road, Street, Flat, Avenue, Cottage, Close, Estate, Farm, etc. We took the top 500 most popular words, and added a series of binary variables to our dataset, corresponding to whether the address contained that particular word or not. We can then use standard modelling techniques to refine the variables, and work out which words (or groupings of words) are significant for our model.

One thing though: we want to capture as much information from the address words as we can, and we’re in the fortunate situation of having lots of data, vertically (that is: lots of rows). So we can split our data not just in to the standard train/test, but we can further split the training data, giving us a validation dataset. [Actually, we’re using the following split: 60% training, 20% validation, 20% test.] With this extra dataset, we can check that a word (variable) is predictive in both the train and validation datasets before we add it to our pool of variables available to the model.

How do we test whether the variable is predictive in both datasets? We could look at the IV (Information Value), or we could model the variable and look at the increase in gini? Both perfectly valid, but I found that I ended up with a larger pool of variables than I was expecting. (There’s a hard time constraint on this piece of work, so I can’t let the modelling procedure take all the time it likes when it comes to selecting variables.) So in order to cut the pool down, I did this:

1. In the training dataset, cross-tab the variable of interest with the dependent (outcome) variable, and calculate the odds ratio (O.R.) and its 95% confidence interval (C.I.).
2. Do exactly the same, but using the validation dataset.
3. If, for each variable:
   • Neither the 95% confidence intervals in the training or validation datasets contains 1 (i.e. we think there is a significant association)
   • And (a) the training O.R. is contained within the validation C.I., and the validation O.R. is contained within the training C.I. (i.e. the variable is not significantly different between datasets)

   , then keep the variable. Otherwise, discard it.

We end up with a far smaller, but significant, selection of variables to let the step-wise modelling process choose from.

Here’s the R function I wrote to obtain the odds ratio and confidence interval from a 2×2 table:

table_OddsRatio <- function(tbl, ci_pct=0.95)
{
	odds_ratio <- (tbl[1,1]*tbl[2,2])/(tbl[1,2]*tbl[2,1]);
	odds_ratio_SE <- sqrt(sum(1/as.vector(tbl))); # Careful, this is SE(log(OR))
	
	value <- qnorm(1.0 - ((1.0-ci_pct)/2));
	
	return(c( OR=odds_ratio,
		CI_lower=exp(log(odds_ratio)-value*odds_ratio_SE),
		CI_upper=exp(log(odds_ratio)+value*odds_ratio_SE))
	);
}

Simple example of its use (numbers taken from sphweb.bumc.bu.edu):

HTN_CVD_tbl <- as.table(matrix(c(992,2260,165,1017),byrow=T,nrow=2));
table_OddsRatio(HTN_CVD_tbl);
      OR CI_lower CI_upper 
2.705455 2.258339 3.241093 

For our data, we just used this function, in conjunction with sapply(), over all the appropriate binary variables in our two data frames (datasets).

In fact, without giving too much away, we didn’t just use this technique for the address data, we had other strings in our dataset we could usefully apply the same process to. One of the reasons I enjoy building models and scorecards so much is that it’s quite a creative endeavour, and you learn something new each time you do it!

Brute-force packing

Because I’m a huge music fan, I own quite a few CDs; rather more than I’d readily admit to! A few years ago, I started ripping my collection to FLAC, a lossless audio format, and backing everything up to DVD-R. In order to be efficient, I want to get as many albums as I can on each DVD-R disc, minimising the space wasted — this is known as a Packing Problem.

Now, I’d love to be able to present you with a highly-optimised algorithm that I wrote, but that’s not what I did: I brute-forced it. Processor cycles are very cheap, and if it’s going to be orders of magnitude quicker to iterate a few million times than it will be to research a whole new area of maths, then iterating it’ll be. My original code was a VB app (so I could drag folders onto a GUI), but here’s a similar version of the code in R:

set.seed(1234);
containerSize <- 4500; # roughly DVD size in MB
itemSize <- c(1641,1498,1747,751,1090,164,1602,1020,1126,553); # album sizes in MB
cat(sprintf("No. containers needed (no partitioning): %5.2f\n", sum(itemSize) / containerSize));

Z <- 1000; # Number of iterations

# To keep track of the best partition
best.remainder <- 1.0;
best.partition <- NULL;

for(i in 1:Z) {

working <- sample(itemSize); # randomly re-order our list of sizes
partition <- list();
k <- 1;
# Using the order as per 'working', partition the items
# such that the container size isn't exceeded:
while (length(working) > 0) {
  this.partition.indexes <- which( cumsum(working) <= containerSize );
  partition[[k]] <- working[this.partition.indexes];
  working <- working[-(this.partition.indexes)];
  k <- k+1;
}
npm1 <- length(partition) - 1; # Number of partitions minus 1
partition.totals <- unlist(lapply(partition, sum));
remainder <- (sum(rep(containerSize, npm1) - partition.totals[1:npm1]))
    / (npm1 * containerSize);

if (remainder < best.remainder) {
  best.remainder <- remainder;
  best.partition <- partition;
  totals.str <- paste("(", paste(partition.totals, collapse=","), ")", sep="");
  partition.str <- paste(unlist(lapply(partition,
      function(x) paste("(",paste(x,collapse=","),")",sep=""))),collapse=",")
  cat(sprintf("i = %3d, rem. = %5.2f%%; totals = %s; partition = %s\n", i,
      remainder * 100.0), totals.str, partition.str));
}

} # end for loop

This code (1000 iterations) runs in the blink of an eye:

i =   1, rem. = 19.00%; totals = (3772,3518,3902);
        partition = (1498,164,1090,1020),(1126,751,1641),(1602,553,1747)
i =   2, rem. = 13.56%; totals = (4439,3341,3412);
        partition = (1602,1090,1747),(553,1498,1126,164),(1641,1020,751)
i =   4, rem. = 13.18%; totals = (3963,3851,3378);
        partition = (1090,1747,1126),(751,1498,1602),(1641,553,164,1020)
i =   6, rem. =  4.78%; totals = (4303,4267,2622);
        partition = (1641,1747,164,751),(553,1126,1498,1090),(1020,1602)
i =  13, rem. =  4.04%; totals = (4301,4335,2556);
        partition = (1020,1126,553,1602),(1747,1498,1090),(751,1641,164)
i =  23, rem. =  0.26%; totals = (4478,4499,2215);
        partition = (1090,1641,1747),(1020,1126,1602,751),(1498,553,164)
i = 524, rem. =  0.02%; totals = (4499,4499,2194);
        partition = (1126,1602,751,1020),(1747,1498,1090,164),(553,1641)

The figure rem. is the percentage of space wasted on the discs that could be full — clearly, not all the discs can be 100% full. So in this case, I knew I was going to be burning three DVD-Rs, but there’s only 1 MB of unused space on each of the first two discs; for the third, I can either find some other files to backup, or keep those two albums to burn later — which is what I usually do; saving even more space, by repeatedly putting off burning the least-full disc.

Upper bound of the Information Value statistic

Information Value

Despite having worked with it for years, it has always irked me that I don’t know the derivation of the Information Value (IV) statistic.

It’s used liberally throughout credit risk work, but the background to its invention seems somewhat hazy. Clearly it’s related to Shannon Entropy, via the construct. In Naeem Siddiqi’s well-known book Credit Risk Scorecards, he writes “Information Value, […] comes from information theory” and references Kulback’s 1959 book Information Theory and Statistics, which I don’t have. Someone else suggested that it stems from the work of I.J. Good, but I can’t find an explicit definition in any of his papers I’ve managed to look at. (I bought his book Good Thinking, about the foundations of probability and statistical interference, but it’s waaaay too complex for me!)

The Information Value (IV) is defined as:

, where is the number of ‘goods’ in category i, and is the number of ‘bads’.

In his book, Siddiqi gives the following rule of thumb regarding the value of IV:

< 0.02	unpredictive
0.02 to 0.1	weak
0.1 to 0.3	medium
0.3 to 0.5	strong
0.5+	“should be checked for over-predicting”

For an independent variable with an IV over 0.5, it might be somehow related to the dependent variable, and you might want to consider leaving it out. (If you build a scorecard that has a bureau score as one of your variables, then you’ll almost certainly see this.)

[See these two links for more about Information Value, and an example or two of its use: All about “Information Value” and Information Value (IV) and Weight of Evidence (WOE).]

Upper Bound

The lower bound of the IV is fairly obviously zero: if for all the categories, then the difference is zero, so their sum is zero times , which is also zero. But what about the upper bound?

I’ve put together this small PDF document: Upper bound of the Information Value (IV), in which (I think!) I show that the upper bound is very close to , where is the total number of goods, and is the total number of bads.

Of course, it’s wise to at least check the result with some code — so in R, let’s create a million tables at random, and look at the actual figures that are produced:

Z <- 1000000; # number of iterations
IV <- rep(0, Z); # array of IVs
lGB <- rep(0, Z); # array of (log(n_g) + log(n_b))

for (i in 1:Z)
{
	k <- sample(2:20, 1); # number of categories
	g <- sample(1:100, k, replace=T); # good
	b <- sample(1:100, k, replace=T); # bad
	ng <- sum(g);
	nb <- sum(b);
	IV[i] <- sum( ((g/ng)-(b/nb)) * log((g/ng)/(b/nb)) );
	lGB[i] <- log(ng) + log(nb);
}
plot(IV, lGB, xlab="IV", ylab="log(N_G)+log(N_B)",
	main="IV vs log(N_G)+log(N_B)", pch=19,col="blue",cex=0.5);
abline(a=0,b=1,col="red",lwd=2); # draw the line x=y

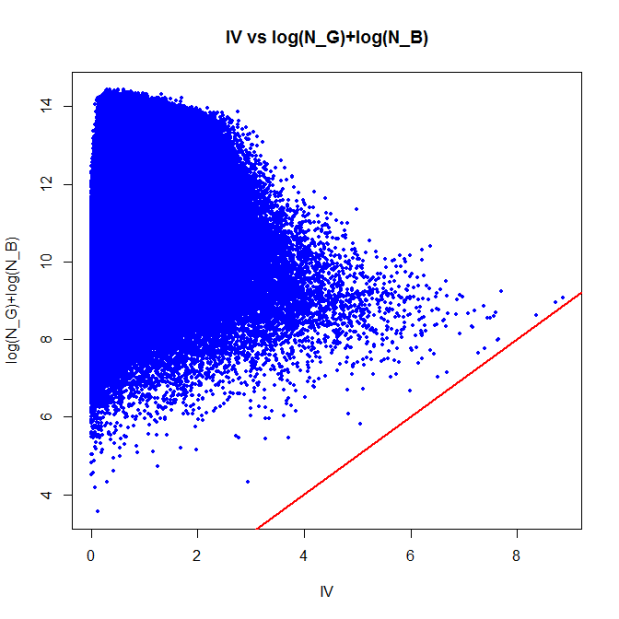
As you can see, there are no points below the red ‘x=y’ line; in other words, the IV is always less than . There are a few points that are close; the closest is:

min(lGB-IV)
[1] 0.2161227

I know that is not the best possible upper bound — a closer, but more complex answer is reasonably obvious from the document — but “log(number of goods) plus log(number of bads)” is (a) memorable, and (b) close enough for me!

Floats may not look distinct

The temporary table #Data contains the following:

SELECT * FROM #Data
GO

value
-------
123.456
123.456
123.456

(3 row(s) affected)

Three copies of the same number, right? However:

SELECT DISTINCT value FROM #Data
GO

value
-------
123.456
123.456
123.456

(3 row(s) affected)

We have the exact same result set. How can this be?

It’s because what’s being displayed isn’t necessarily what’s stored internally. This should make it clearer:

SELECT remainder = (value - 123.456) FROM #Data
GO

remainder
----------------------
9.9475983006414E-14
1.4210854715202E-14
0

(3 row(s) affected)

The numbers aren’t all 123.456 exactly; the data is in floating-point format, and two of the values were ever-so-slightly larger. The lesson is: be very careful when using aggregate functions on columns declared as type float.

Some other observations:

• The above will probably be reminiscent to anyone who’s done much text wrangling in SQL. Strings look identical to the eye, but different to SQL Server’s processing engine; you end up having to examine every character, finding and eliminating extraneous tabs (ASCII code 9), carriage returns (ASCII code 13), line-feeds (ASCII code 10), or even weirder.
• If your requirement warrants it, I can thoroughly recommend the GNU Multiple Precision Arithmetic Library, which stores numbers to arbitrary precision. It’s available as libraries for C/C++, and as the R package gmp:

# In R:

> choose(200,50);  # This is 200! / (150! 50!)
[1] 4.538584e+47
> library(gmp);
Attaching package: ‘gmp’
> chooseZ(200,50);
Big Integer ('bigz') :
[1] 453858377923246061067441390280868162761998660528

# Dividing numbers:
> as.bigz(123456789012345678901234567890) / as.bigz(9876543210)
Big Rational ('bigq') :
[1] 61728394506172838938859798528 / 4938271605
# ^^ the result is stored as a rational, in canonical form.